HOW TO ADJUST THE FOCAL LENGTH ?
To reach the large focal lengths required in high resolution imaging, focal extenders are used: Barlow lenses and eyepieces. Barlow lenses and eyepieces are not competitors, they are complementary: the first are used for moderate amplification factors (typically 2x to 4x), the second for large amplification factors (6x or more). On the other hand, in deep-sky imaging, focal reducers are useful to decrease to exposure times and increase the field of view.
The calculations of resultant focal length are simple, they need only a four-operation calculator and a graduated ruler.
Barlow lens projection
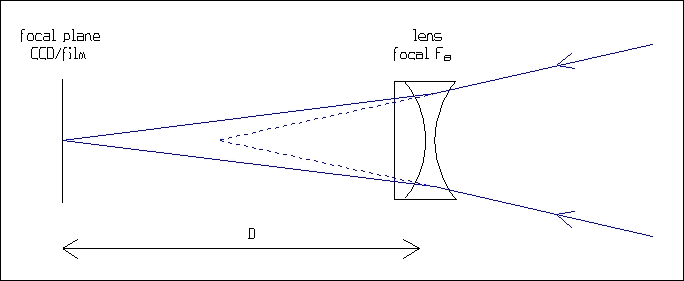
A Barlow lens is a group of lenses with a negative power, which amplifies the primary focal length of the telescope. Its amplification factor is usually written on its tube: 1.8x, 2x, 2.5x, 3x, etc. An important point is that this factor is true only for a specific distance between the lens and the focal plane (film or CCD detector). If this distance changes, the amplification factor changes.

The relation between the amplification factor A, the focal length FB of the Barlow lens and the distance D between the lens and the focal plane is:
|
A = D/FB + 1 |
(actually, the focal length of a divergent lens has a negative value, but here we consider its absolute value).
Example: a Barlow lens, whose focal length is 100 mm, is installed at a distance of 150 mm from the CCD detector (or the film). Its amplification factor is A = 150/100 + 1 = 2.5x. On a 200 mm F/D 10 telescope, the final focal length is 2000*2.5 = 5000 mm, and the final focal ratio is 10*2.5 = 25.
The formula shows that when the distance increases, the amplification factor increases, and that a '2x' Barlow lens gives an true amplification factor of 2 only if its distance from the focal plane is equal to its focal length (100 mm in the previous example). If this distance is doubled, the amplification factor becomes 3x.
Once the resultant focal length of the telescope is chosen, the amplification factor must be adjusted to reach this value, by changing the distance between the Barlow lens and the focal plane. The formula can be reversed to obtain D from A and FB: D = FB (A - 1)
In the previous example, if the required focal length of the telescope is 6200 mm, the amplification factor must be 6200/2200 = 2.8x. The distance between the CCD detector (or the film) and the lens, whose focal length is 76 mm, must be D = 76*(2.8 - 1) = 137 mm.
The best way of using a Barlow lens is unscrewing to lens part from the part which receives the eyepiece, and inserting it in a 42mm photographic eyepiece adaptor. Although this methods allows to move a bit the lens inside the adaptor, some rings of different lengths may be needed to reach the desired distance between the lens and the focal plane.
Calibration of a Barlow lens
Unfortunately, the focal length of a Barlow lens is not usually known a priori. Therefore, it must be determined from images of a known object, a planet or a couple of stars for example. The method is:
1. take an image of a planet whose angular diameter P (in arcsec) is known from ephemerides
2. measure the size of its image S (in microns) on the detector or the film
3. calculate the resultant focal length F (in millimeters) with the 'sampling' formula: F = 206 S/P
4. take another image of the same object, but now without Barlow lens: the same formula gives the primary focal length FP of the telescope
5. calculate the amplification factor of the Barlow lens: A = F/ FP
6. measure the distance D (in millimeters) between the lens and the focal plane
7. calculate the focal length FB of the Barlow lens with the formula: FB = D / (A - 1)
Example: an image of Jupiter, whose size is 46", is taken with a KAF-0400 CCD detector (9 microns pixels) behind a Barlow lens. The size of the planet is 170 pixels, corresponding to 170*9 = 1530 microns. The resultant focal length of the telescope is F = 206*1530/46 = 6850 mm. Without the Barlow lens, the size of the image is 55 pixels (495 microns), corresponding to a primary focal length of the telescope FP = 206*495/46 = 2200 mm. The amplification coefficient is A = 6850/2200 = 3.11x. The distance between the Barlow lens and the CCD detector is 160 mm, then the focal length of the lens is FB = 130/(3.11 - 1) = 76 mm.
Specially with SCTs, measuring the real primary focal length of the telescope is a good precaution, because this focal length varies according to the position of the primary mirror (the secondary mirror, whose role is to amplify the focal length of the primary mirror, behaves like a Barlow lens).
Combination of Barlow lenses
Due to aberration correction problems, a Barlow lens doesn't work in good conditions at any amplification factor. For example, a '2x' Barlow lens works correctly between 2x and 3x, but not at 5x or 6x. These large amplification factors can be obtained with the help of a series of two Barlow lenses whose amplification factors will be multiplied.
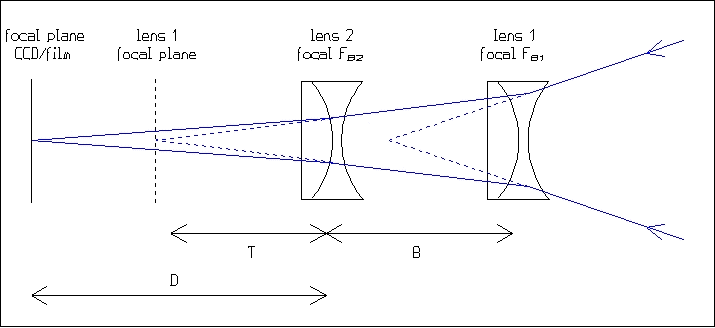
The calculations are:
1. given the focal length FB2 of the Barlow lens 2 (the closest to the focal plane) and its distance D from the focal plane, calculate its amplification factor A2
2. the distance between the lens 2 and the focal plane relating to the lens 1 is T = D/A2
3. given the distance B between the two lenses, the distance between the lens 1 and its focal plane is T + B
4. calculate the amplification factor A1 of the lens 1 with its focal length FB1 and the distance T + B
5. the resultant amplification factor is A = A1 * A2
Example: two identical Barlow lenses whose focal length is 76 mm, are separated by a distance of 50 mm. The distance between the lens 2 and the CCD detector is 100 mm. Its amplification factor is A2 = 100/76 + 1 = 2.3x. The distance between the lens 2 and the focal plane relating to the lens 1 is 100/2.3 = 43 mm. The distance between the lens 1 and its focal plane is 43 + 50 = 93 mm. The amplification factor of the lens 1 is A1 = 93/76 + 1 = 2.2x. The final amplification factor A of the combination of lenses is A = 2.3*2.2 = 5.1x.
Eyepiece projection
An standard visual eyepiece is designed to give parallel rays. But when it is used in photographic or CCD projection, it gives a convergent beam. Therefore, because of aberrations correction problems (specially field curvature), it works correctly only at large amplification factors, typically 6x or more.
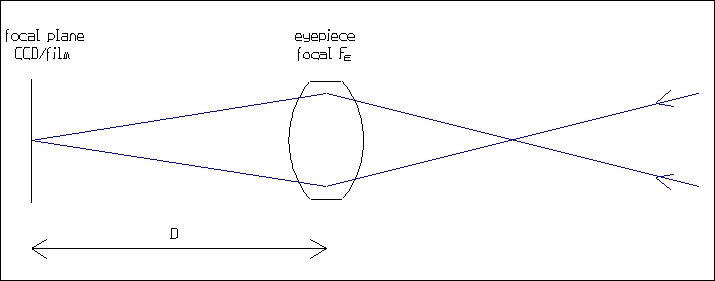
The relation between the focal length FE of the eyepiece, the amplification factor A and the distance D between the eyepiece and the focal plane is:
|
A = D/FE - 1 |
Example : a 20 mm eyepiece, installed at 180 mm from the focal plane, gives an amplification factor of A = 180/20 - 1 = 8x.
focal reducer
A focal reducer is a group of lenses with a positive power, which decreases the primary focal length of the telescope. As in the case of a Barlow lens, its reduction factor depends on its focal length and its distance from the focal plane. When this distance increases, the reduction is more pronounced. Because of aberration correction problems, it is advised to use a focal reducer at a reduction factor very close to its nominal factor.
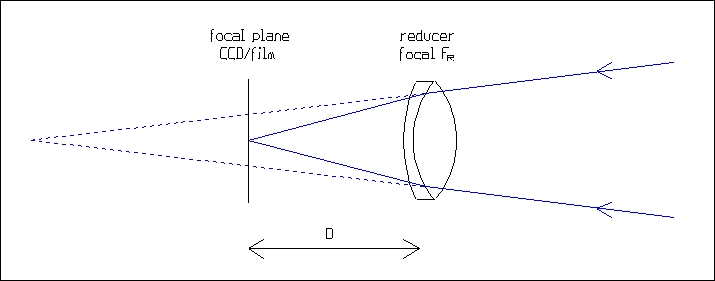
The relation between the reduction factor R, the focal length FR of the reducer and the distance D between the lens and the focal plane is:
|
R = 1 - D/FR |
Determining the focal length of a focal reducer is easy: point the Sun (or the Moon) with the reducer alone, and measure the distance between the lens and the solar (or lunar) image.
The Meade/Celestron F/6.3 reducer has a focal length of about 230 mm. Therefore, the nominal distance between the lens and the focal plane is about D = FR*(1 - R) = 230*(1 - 0.63) = 85 mm. It is only at this distance that this reducer gives its nominal reduction factor of 0.63x.
The drawing above shows that a focal reducer moves the focal plane closer to the telescope. On some instruments, the focusing range may not be sufficient to reach the point with a focal reducer. Furthermore, specially on SCTs, vignetting problems are usually more critical with a reducer than without.