Un instrument optique vise une mire composée de traits alternativement blancs et noirs (figure 1) dont l'espacement est réglable. Au foyer de l'instrument, l'image de la mire est retrouvée (figure 2), mais les bords des traits ne sont plus aussi nets et le contraste a diminué : les noirs sont devenus gris foncé, les blancs gris clair.

Le rapport entre le contraste de l'image (C_i) et le contraste de la mire (C_m) est une excellente indication de la qualité de retransmission de l'information par l'instrument. Dans l'idéal, ce rapport serait de 1 : image identique à l'objet. Malheureusement, la théorie de la diffraction de la lumière nous apprend qu'au foyer d'un instrument l'image d'un point lumineux tel qu'une étoile n'est pas un point mais une figure dont la dimension n'est pas nulle, ce qui implique qu'un instrument même parfait est incapable de retransmettre l'information avec une fidélité absolue. Le rapport C_i/C_m est donc toujours inférieur à 1.

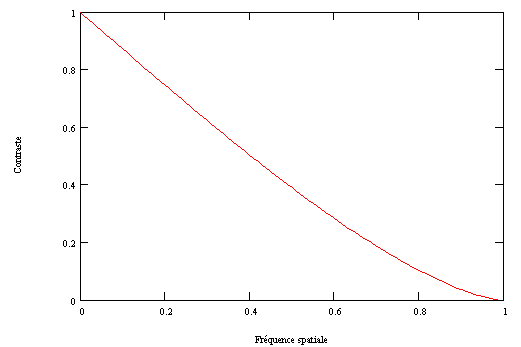
La courbe ci-dessus représente la valeur de ce rapport en fonction de l'espacement des traits de la mire, pour un instrument optiquement parfait et non obstrué. Lorsque les traits sont très larges (leur fréquence spatiale est petite), l'instrument retransmet fidèlement l'image : le rapport de contraste est voisin de 1 (extrémité gauche de la courbe). Puis, lorsque les traits se rapprochent (leur fréquence spatiale augmente), le contraste diminue (partie centrale de la courbe). Finalement, lorsque les traits sont très rapprochés (fréquence spatiale élevée), l'instrument n'est plus capable de les séparer : l'image est une plage grise uniforme, sans aucun détail (extrémité droite de la courbe). La limite de résolution de l'instrument est atteinte. La valeur de cette fréquence limite ne dépend que de la longueur d'onde de la lumière (l) et du diamètre de l'instrument (D), elle vaut (en paires de lignes par radian) :

F_max = D/l

Pour un instrument d'un diamètre de 250 mm, à 0,6 µm cette limite correspond à 2 paires de lignes par seconde d'arc, soit 1 trait (blanc ou noir) pour 1/4 de seconde d'arc.

Cette fréquence limite s'accroît lorsque la longueur d'onde diminue ou lorsque le diamètre de l'instrument augmente. La figure suivante représente les courbes de Fonction de Transfert de Modulation (FTM, ou MTF en anglais) relatives à deux instruments parfaits dont l'un a un diamètre double de l'autre. L'instrument de plus grand diamètre est capable de montrer des détails plus fins, sa limite de résolution théorique est deux fois plus élevée.

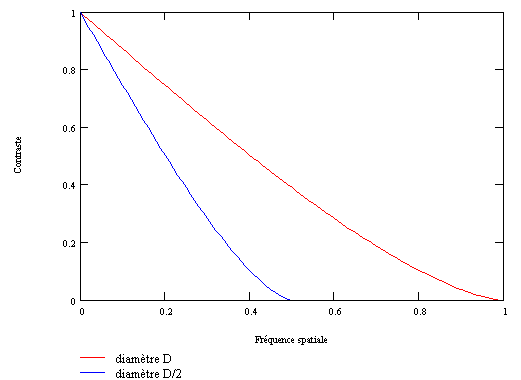
Bien que les objets astronomiques ne ressemblent pas à une mire de traits blancs et noirs, ce type de courbe fournit de précieuses informations à propos des performances d'un instrument sur les objets célestes tels qu'une planète ou la Lune, puisqu'elle indique comment l'instrument retransmet les contrastes. Le balayage des différentes fréquences spatiales permet d'observer le comportement de l'instrument sur des détails de différentes échelles, les fréquences basses correspondant aux détails larges et les fréquences hautes aux détails fins. Ce type de représentation permet également de visualiser les conséquences de tous les types d'aberrations pouvant affecter l'instrument, et même d'en simuler l'effet sur des images réelles.