There are many things that image processing can do...and some things that it cannot !

In high resolution field, in addition to the usual preprocessing functions (offset, dark and flat corrections), the usefulness of image processing can be divided into two main functions: increasing the contrast of planetary details and reducing the noise.

On a planet, the contrast of details is generally small compared to the brightness of the disk. Then, a raw planetary image directly displayed on a computer display shows few details because close details occupy only one grey level. We need to increase the contrast of the details to make them clearly visible on the screen.

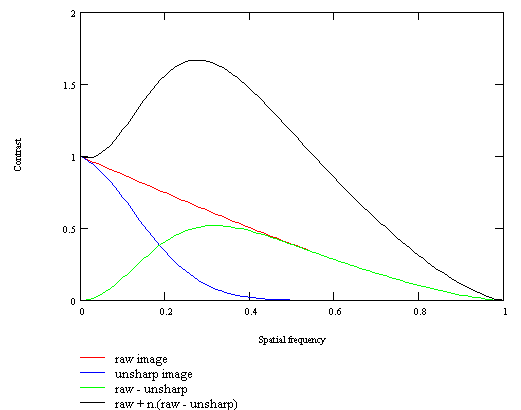
Increasing the contrast of small details is the aim of many processing algorithms which all act in the same way: they amplify the high frequencies in the image. This is the reason why they are called high-pass filters, and probably the most famous of them is unsharp masking. This technique is well-known but hard to use in astrophotography. In digital image processing the general principle of unsharp masking is (figure below, see What is a MTF curve ?):

- a fuzzy image (blue curve) is made from the initial image (red curve) by application of a low-pass filter (gaussian) whose strenght is adjustable; the high frequencies are suppressed,

- this fuzzy image is substracted from the initial image; the result (green curve) contains only the small details (high frequencies) but its appearance is very strange and unaesthetic (unfortunately, this image also contains noise),

- this last image is multiplied by an adjustable coefficient (usually between 2 and 10), and added to the initial image. The result (black curve) is an image whose appearance is 'normal' but where small-scale details (high frequencies) have been amplified.

This kind of filter is very efficient but unfortunately it is not without its drawbacks.

First, the Gibbs effect: artefacts can appear in some areas of the processed image, specially where there are sharp variations of brightness: the edge of a planet, the shadow of a satellite on Jupiter, the Cassini division, etc...On these places, this effect can be seen as dark rings around bright areas or bright rings around dark areas. On details like the shadow of a satellite on Jupiter, the effect is easily recognizable by a bright ring around the shadow. But on more complex details this effect can be very difficult to detect. Nevertheless it can be present and create 'false' details that are very difficult to separate from the 'true' details. Unfortunately, since they are associated with real details, these artefacts appear in a same way on every processed image. The only way to reduce the risk of such an effect is to limit as much as we can the strenght of the processing, and it is possible only if the contrast is high enough in the raw image.

The other annoying consequence of high-pass filters concerns the noise. In a raw image the noise is mainly located in the high frequencies. Just like details that are amplified by high-pass filters ! Since it is impossible to separate signal from noise, both are amplified in the same way, and the result can be an image where noise and details are so mixed up that it is impossible to distinguish between them. Sometimes the image seems to be very detailed but a comparison with better images (like HST ones) show that actually it is dominated by noise ! This is the reason why noise must be reduced before applying any processing.

Considering the high levels brightness, in a raw planetary (or lunar) image the noise is widely dominated by the photon noise (in most of the cases other noises are negligible). The photon noise comes from the light of the object itself (the signal) and is due to the discrete nature of the light. In a raw image, statistical laws say that the average level of noise is proportional to the square root of the signal. Therefore the signal-to-noise ratio is itself proportional to the square root of the signal.

Example: on a planetary image made with a camera whose A/D converter saturation level is 50000 electrons, the average level of brightness on a planetary surface is about 30000 electrons. The average amount of noise in such an image is about 170 electrons. Then the signal-to-noise ratio is 170.

On a computer display with 64 grey levels, the noise is generally invisible in the raw image because its average level is less than one grey level (signal-to-noise ratio over 100). But, as seen before, the noise is amplified by high-pass filters and becomes obvious after such a processing. In the previous example, if the amplification coefficient of the unsharp mask is 8, the signal-to-noise ration falls to about 20, and the noise occupies several grey levels on the screen. Now the noise is clearly visible and it is mixed up with details.

Unfortunately, in a single image, noise cannot be reduced because it is not separable from the signal. But, thanks to its ramdom nature, the noise is different from one image to the next. Adding four images multiplies the signal by a factor of 4 and the noise by a factor of only 2. Then the signal-to-noise ratio has been multiplied by a factor of 2. In the previous example, combining 10 images multiplies this ratio by 3.3: its value becomes 560 in the composite image, and 70 in the final processed image. The image is very smooth on the screen, and the true details are more easily visible (again, beware of processing artefacts !).

Examine the images below. The first image (top left) is an single raw image of Jupiter. The second image (top right) is a composition of 15 raw images. Both are smooth, the difference between them is invisible. But after unsharp masking (bottom), the difference becomes clear: the second image is smoother than the other, and we can see more details because they emerge from the noise.

In deep-sky imaging it is even more difficult to use processings like unsharp masking or restorations (Ridcharson-Lucy, maximum entropy, etc...) because the undesirable effects described before are stronger. The signal-to-noise ratio is lower than in planetary images, so the noise is tremendously amplified, and the artefacts, specially dark rings aroud stars, give to the image an unpleasant appearance. Again, the best way to avoid these problems is to obtain good quality raw images.

Some people, probably by analogy with special effects in movies, think that astronomical image processing is so efficient that it can correct problems at the telescope like bad seeing, bad or misaligned optics, bad focusing, bad guiding, etc... It is a legend. The role of image processing is not to invent the details that have disappeared at the telescope, it is to transform an image in the aim of seeing better the details inside...if there are details ! It is impossible to obtain a good processed image from a poor raw image, just like in astrophotography it is impossible to transform a bad negative into a good printing. Of course, because details are not easily visible in a raw planetary image, the visual difference between a good raw image and a bad raw image may be difficult to see. But after processing the difference between them becomes enormous because image processing cannot create details from scratch (see images below). The largest efforts of processing are not worth the smallest improvement at the telescope : when the photons reach the CCD, the die is cast ! Image processing can do admirable things...but no miracles !

Furthermore, an astronomical image is something fragile, and it is dangerous (and unuseful) to torture it to extract details. Image processing softwares are now so powerful that they look like Ferraris...but don't drive them like Ayrton Senna ! Actually the best is to process an image as little as possible: the first quality of an amateur in this field is its moderation. Just take a look at the planetary images of the HST: they are detailed but very smooth and natural, no trace of the over-processing that damages so many amateur images. If a raw image is good, a slight processing must be sufficient for showing its contents. And if a processed image shows too few details, it is not a problem of processing but a problem of acquisition.